Replace derivatives in back propagation

When I tried to calculate the derivative of ReLU, i.e.

$Y = max(0, X)$

where Y, X are (N, H) dimension matrix, I was astounded. Isn’t it a 4-dimension array of shape (N, H, N, H)?

Actually it is. But according to this document by Erik Learned-Miller,

Dealing with three[or four for here]-dimensional arrays, it becomes perhaps more trouble than it’s worth to try to find a way to display them. Instead, we should simply define our results as formulas which can be used to compute the result on any element of the desired three dimensional array

Which says, condensing the derivative ‘tensor monsters’ into a simple formula is not only possible, but also an important trick when back-prop through the neural networks.

1. Derivative of ReLU
   1. Element-wise analysis
   2. Take it back to Matrix
   3. Implement in code
   4. So did you simplified $\mathrm{d}Y/\mathrm{d}X$ ?
2. More backprop calculation
   1. Affine layer
   2. Batch Norm layer
3. To generalize

Derivative of ReLU

So let’s read the document and use it to solve the problem at the beginning.

Let our final loss to be $L$, then you may write

but it helps nothing! What is $\mathrm{d}Y/\mathrm{d}X$ anyway?

so we have to rewrite it, element wise.

Element-wise analysis

and as $\mathrm{d}Y_{k,l}/\mathrm{d}X_{i,j} = 0, \forall (k, l) \neq (i, j) $, it reduces to

Take it back to Matrix

Now we are ready to reduce the $\mathrm{d}Y/\mathrm{d}X$ monster.

\(\mathrm{d}L/\mathrm{d}X = (\mathrm{d}L/\mathrm{d}X_{i,j})_{i,j} = (\mathrm{d}L/\mathrm{d}Y_{i,j} \cdot 1(X_{i,j}> 0))_{i,j}\) \(= \mathrm{d}L/\mathrm{d}Y * 1(X > 0)\)

Here $*$ denote element-wise product between matrices.

Implement in code

As is shown in this lecture note

the ReLU unit lets the gradient pass through unchanged if its input was greater than 0, but kills it if its input was less than zero during the forward pass.

so the code implementation would be

# backprop the ReLU non-linearity
dhidden[hidden_layer <= 0] = 0

So did you simplified $\mathrm{d}Y/\mathrm{d}X$ ?

No, I didn’t. $\mathrm{d}Y/\mathrm{d}X$ is still the monster as it is.

What I did above is using a new matrix to replace the original matrix without loss of information. Actually it simply accelerate the calculation.

As you can see, the original matrix-dot manipulation is even replaced by a element-wise product. But it doesn’t matter.

More backprop calculation

Affine layer

and $\mathrm{d}Y/\mathrm{d}b$ actually needs more care, because actually a broadcast is going on here.

Batch Norm layer

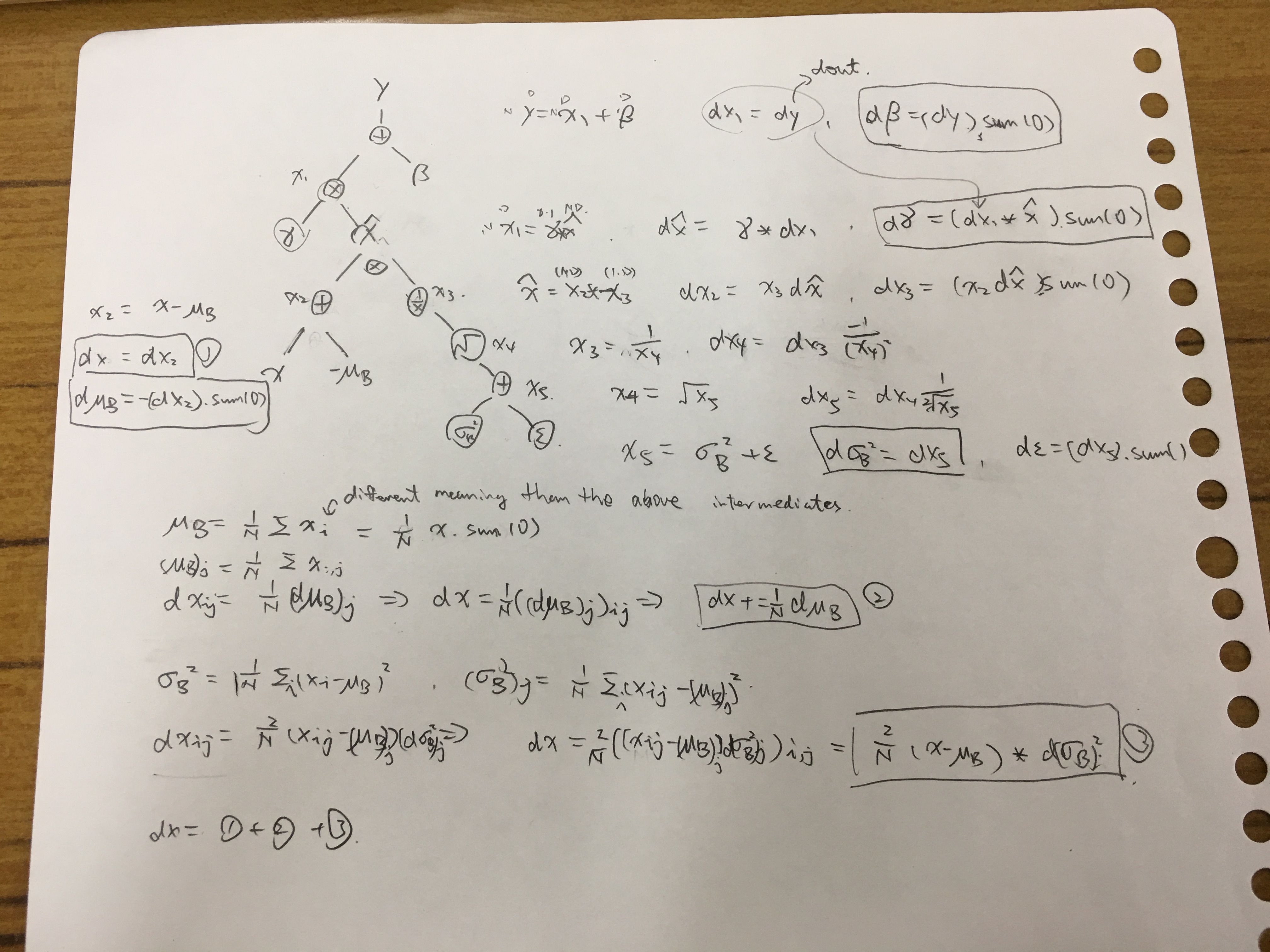
To generalize

Representing the important part of derivative arrays in a compact way is critical to efficient implementations of neural networks.

We are looking for a map $f_\frac{\mathrm{d}Y}{\mathrm{d}X}$ s.t.

and $f_\frac{\mathrm{d}Y}{\mathrm{d}X}$ should be as simple and quick to calculate as possible.